HiLLS
HiLLS stands for High Level Language for System Specification, a graphical formalism that allows to describe the structure and behaviour of a system.
It is defined with the following elements M = < X, Y, Λ, Φ, Σ, Δ > where
- X is the input
- Y is the output
- Λ is the set of parameters
- Φ is the set of phases
- Σ is the semantic domain
- Δ is the set of transitions
The parameters actually define the context in which the system evolves, they are the information associated to the system and its environment. A phase is a set of states , grouped together according to a given subjective criterion. If we represent the system as an automaton, they are the nodes. In that case, Δ is the set of the edges of the automaton, they are called transitions.
 Fig.1 - A simple example with 3 phases and 3 transitions.
Fig.1 - A simple example with 3 phases and 3 transitions.
A phase φ ∈ Φ can be written as φ = < invariant, activity, duration > where invariant characterizes what defines the phase, the state variables on the semantic domain (e.g. temperature, pressure, ...), activity is the result of a computation associated to the current phase, duration refers to the sojourn time of the phase that belongs to [0, +∞]. Any phase can be
- normal, its sojourn time is 0 < t < +∞, it is represented as a regular line
- passive, its sojourn time is +∞, it is represented as a double line
- transient, its sojourn time is null, it is represented as a dotted line
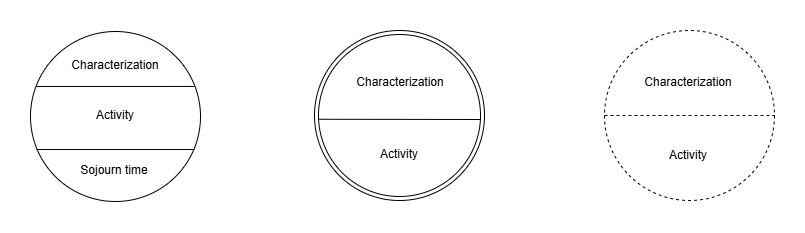 Fig.2 - The three differend kinds of phases: normal, passive and transient
Fig.2 - The three differend kinds of phases: normal, passive and transient
A transition δ ∈ Δ is defined between two phases. Any transition can be
- internal, where the sojourn time is finite (when the sojourn time has elapsed, an output message can then be generated), it is represented as a regular line
- external, when an exterior event causes the change (an input message is sent to the system), it is represented as a dotted line
- confluent, when the occurrence of an exterior event is coincident with the sojourn time elapsing, it is represented as a regular dotted line


 Fig.3 - The three differend kinds of transitions: internal, external and confluent
Fig.3 - The three differend kinds of transitions: internal, external and confluent
- Aliyu, H.O. & Maïga, O. & Traoré, M.K. (2016) The high level language for system specification:
A model-driven approach to systems engineering. International Journal of Modeling, Simulation,
and Scientific Computing. DOI : 10.1142/S1793962316410038
- Maïga, O., Aliyu, H. O., & Traoré, M. K. (2015). A New Approach to Modeling Dynamic
Structure Systems. European Simulation Modeling Conference, pp. 11–18
- Samuel, K. G., Maïga, O., & Traoré, M. K. (2019). Formal verification with HiLLS-specified
models : A further step in multi-analysis modeling of complex systems. International Journal of Modeling, Simulation, and Scientific Computing, 10(5), 1950032. DOI :
10.1142/S1793962319500326





